详解数据结构八大排序算法

最近在复习刷一些算法题，做到了排序题，就顺便整理下数据结构中的八大排序算法。
首先解释下算法的稳定性定义：对于待排序列中相同项的原来次序不能被算法改变则称该算法稳定。
八大排序的稳定性，时间复杂度、空间复杂度、稳定性总结如下图：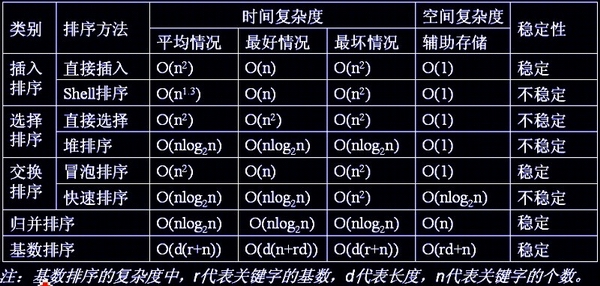

其中STL中的sort函数原理是：在数据量大的时候采用快速排序，分段后的数据量小于某一个门槛时便采用直接插入排序。

1.直接插入排序

思路：每次将一个待排序的元素按大小插入到前面已经排过序的序列中的合适位置，直到数据全部插入为止。
时间复杂度：O(n^2)
空间复杂度：O(1)
稳定性：稳定

void insert_sort (int arr[], int n) {
    // 从小到大排序
    for (int i = 1; i < n; i++) {
        int temp = arr[i];
        for (int j = i - 1; j >= 0 && arr[j] > temp; j--) {
            // 待插入元素小于已有的，就将已有的向后挪，直到元素大于插入元素或已经到达序列最前端
            arr[j + 1] = arr[j];
        }
        arr[j + 1] = temp;
    }

}

2.Shell排序

思路：希尔排序是对直接插入排序算法的改进。先取一个小于n的整数h1作为第一个增量，把全部数据分成h1个组。先在各组内进行直接排序，然后取第二个增量h2 < h1重复上面的分组和排序，直至所取的增量ht = 1(ht < ht-1 < … < h2 < h1),即所有记录放在同一组中进行直接排序为止。
时间复杂度：O(n^2)
空间复杂度：O(1)
稳定性：不稳定
对Sell排序更具体的描述和图解样例可在此点击查看

void shell_sort (int arr[], int n) {
    for (int h = n / 2; h > 0; h /= 2) {
        for (int i = h; i < n; i++) {
            int temp = arr[i];
            for (int j = i - h; j >= 0 && arr[j] > temp; j -= h) {
                arr[j + h] = arr[j];
            }
            arr[j + h] = temp;
        }
    }
}

3.冒泡排序

思路：从数组开头进行遍历，元素两两比较，若位置不对，即交换位置。
时间复杂度：O(n^2)
空间复杂度：O(1)
稳定性：稳定

void bubble_sort (int arr[], int n) {
    // 从小到大排序,一共排序n次，每次找到剩下最大的数提到后面
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n - 1 - i; j++) {
            if (a[j] > a[j + 1]) {
                int temp = a[j];
                a[j] = a[j + 1];
                a[j + 1] = temp;
            }
        }
    }
}

4.快速排序

思路：对冒泡排序的改进，通过一趟排序将数据分为2份，其中一部分所有数据都比另一部分的要小，然后按此方法再对两列数据进行快排，递归进行。

递归实现

具体步骤：

1. 从数列中挑出一个元素，称为 “基准”（pivot）。
2. 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作。
3. 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

时间复杂度：O(nlogn), 最坏情况为O(n^2)
空间复杂度：O(nlogn), 最坏情况为O(n)
稳定性：不稳定

void recurive_quick_sort (int arr[], int left, int right) {
    if (left < right) {
        // 用数组的第一个记录作为枢轴
        int pivot = arr[left];
        int low = left;
        int high = right;
        while (low < high) {
            while (low < high && arr[high] >= pivot) {
                high--;
            }
            arr[low] = arr[high];
            while (low < high && arr[low] <= pivot) {
                low++;
            }
            arr[high] = arr[low];
        }
        arr[low] = pivot;
        recurive_quick_sort(arr, left, low - 1);
        recurive_quick_sort(arr, low + 1, right);
    }
}

非递归实现

具体步骤：

1. 申请一个栈，存放排序数组的起始位置和终点位置。
2. 将整个数组的起始位置start和终点位置end进栈
3. 出栈数据，对出栈的数据进行排序，查找基准数据所在最终的位置 pivot。
4. 判断起始位置start是否小于基准位置pivot-1，如果小于则将起始位置和pivot-1为终点位置进栈
5. 判断基准位置pivot+1 是否小于终点位置end,如果小于则将 pivot+1作为起始位置，end作为终点位置进栈
6. 判断栈是否为空，如果不为空则重复第三步，否则退出操作。

int partition (int arr[], int start, int end) {
    int pivot = a[start];
    while (start < end) {
        while (start < end && arr[end] >= pivot) {
            end--;
        }
        arr[start] = arr[end];
        while (start < end && arr[start] <= pivot) {
            start++;
        }
        arr[end] = arr[start];
    }
    arr[start] = pivot;
    return start;
}

void non_recurive_quick_sort (int arr[], int n) {
    vector<int> v;
    v.push(0);
    v.push(n);
    while (!v.empty()) {
        int right = v.pop();
        int left = v.pop();
        if (left > right) continue;
        int n = partition(arr, left, right);
        if (left < i - 1) {
            v.push(left);
            v.push(i - 1);
        }
        if (right > i + 1) {
            v.push(i + 1);
            v.push(right);
        }
    }
}

5.直接选择排序

思路：进行n-1次排序，每次在剩下的元素中选择最小(大)的元素放到已排好序元素的后面
时间复杂度：O(n^2)
空间复杂度：O(1)
稳定性：不稳定

void select_sort (int arr[], int n) {
    for (int = 0; i < n - 1; i++) {
        int minIndex = i;
        for (int j = i + 1; j < n; j++) {
            if (arr[minIndex] > arr[j]) {
                minIndex = j;
            }
        }
        if (i != minIndex) {
            int temp = arr[minIndex];
            arr[minIndex] = arr[i];
            arr[i] = temp;
        }
    }
}

6.堆排序

思路：利用heap这种数据结构(可看成一个完全二叉树)，使在排序中比较的次数明显减少。
具体步骤：

1. 第1趟将索引0至n-1处的全部数据建大顶(或小顶)堆，就可以选出这组数据的最大值(或最小值)。将该堆的根节点与这组数据的最后一个节点交换，就使的这组数据中最大(最小)值排在了最后。
2. 第2趟将索引0至n-2处的全部数据建大顶(或小顶)堆，就可以选出这组数据的最大值(或最小值)。将该堆的根节点与这组数据的倒数第二个节点交换，就使的这组数据中最大(最小)值排在了倒数第2位。
3. …
4. 第k趟将索引0至n-k处的全部数据建大顶(或小顶)堆，就可以选出这组数据的最大值(或最小值)。将该堆的根节点与这组数据的倒数第k个节点交换，就使的这组数据中最大(最小)值排在了倒数第k位。

其实整个堆排序过程中, 我们只需重复做两件事：

1. 建堆(初始化+调整堆, 时间复杂度为O(n));
2. 拿堆的根节点和最后一个节点交换.

时间复杂度：O(nlogn)
空间复杂度：O(1)
对堆排序更具体的描述和图解样例可在此点击查看

void heap_sort (int arr[], int n) {
    // 创建最大堆，从最后一个节点的父节点开始
    int start = n / 2 - 1;
    for (int i = start; i >= 0; i--) {
        maxHeap(arr, n, i);
    }
    // 排序：末尾与头交换，逐一找出最大值，最终形成一个递增的有序序列
    for (int i = n - 1; i > 0; i--) {
        int temp = arr[0];
        arr[0] = arr[i];
        arr[i] = temp;
        maxHeap(arr, i, 0);
    }
}

void maxHeap (int arr[], int len, int index) {
    int left = 2 * index + 1; // 左子节点
    int right = 2 * index + 2; // 右子节点
    int maxIndex = index; // 最大元素下标
    // 分别比较当前节点和左右子节点，找出最大值
    if (left < len && arr[maxIndex] < arr[left]) maxIndex = left
    if (right < len && arr[maxIndex] < arr[right]) maxIndex = right
    if (maxIndex != index) {
        int temp = arr[index];
        arr[index] = arr[maxIndex];
        arr[maxIndex] = temp;
        maxHeap(arr, len, maxIndex);
    }
}

7.归并排序

思路：即将两个已经排序的序列合并成一个序列的操作。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。
具体步骤：

1. 申请两个与已经排序序列相同大小的空间，并将两个序列拷贝其中；
2. 设定最初位置分别为两个已经拷贝排序序列的起始位置，比较两个序列元素的大小，依次选择相对小的元素放到原始序列；
3. 重复2直到某一拷贝序列全部放入原始序列，将另一个序列剩下的所有元素直接复制到原始序列尾。

时间复杂度：O(nlogn)
空间复杂度：O(n)
对归并排序更具体的描述和图解样例可在此点击查看

void merge_sort (int arr[], int low, int high) {
    if (low < high) {
        int mid = (low + high) / 2;
        merge_sort(arr, low, mid); // 将左边递归排序
        merge_sort(arr, mid + 1, high); // 将右边递归排序
        merge(arr, low, mid, high); // 合并两个序列
    }
}

void merge (int arr[], int low, int mid, int high) {
    int temp[high - low + 2];
    int i = low;
    int j = mid + 1; // 避免重复比较arr[mid]
    int k = 0;
    while (i <= mid && j <= high) { //数组arr[low,mid]与数组(mid,high]均没有全部归入数组temp中去
        if (arr[i] <= a[j]) temp[k++] = arr[i++] // 如果arr[i]小于等于arr[j],则将arr[i]的值赋给temp[k]，之后i,k各加一，表示后移一位
        else temp[k++] = arr[j++] // 否则，将arr[j]的值赋给temp[k]，j,k各加一
    }
    while (i <= mid) { // 表示数组arr(mid,high]已经全部归入temp数组中去了，而数组arr[low,mid]还有剩余
        temp[k++] = arr[i++] // 将数组arr[low,mid]剩下的值，逐一归入数组temp
    }
    while (j <= high) { // 表示数组arr[low,mid]已经全部归入到temp数组中去了，而数组(mid,high]还有剩余
        temp[k++] = arr[j++] // 将数组arr(mid,high]剩下的值，逐一归入数组temp
    }
    for (i = 0; i < k; i++) { // 将归并后的数组的值逐一赋给数组arr[low,high]
        arr[low + i] = temp[i] // 注意，应从arr[low+i]开始赋值
    }
}

8.基数排序

思路：将所有待比较数值（正整数）统一为同样的数位长度，数位较短的数前面补零。然后，从最低位开始，依次进行一次排序。这样从最低位排序一直到最高位排序完成以后, 数列就变成一个有序序列。
具体步骤：

1. 将数组按照个位数进行排序
2. 将1得到的数组按照十位数进行排序
3. …
4. 将上一步得到的数组按照数组存在数字的最高位进行排序
   时间复杂度：O(d(r + n))
   空间复杂度：O(rd + n)

r代表关键字基数，d代表长度，n代表关键字个数
对基数排序样例可在此点击查看

int maxbit (int arr[], int n) // 求数组内的最大位数
{
    int d = 1;
    int p = 10;
    for (int i = 0; i < n; i++) {
        while (arr[i] >= p) {
            p *= 10;
            d++;
        }
    }
    return d;
}

void radix_sort (int arr[], int n) {
    int d = maxbit(arr, n);
    int tmp[n + 1];
    int count[10];
    int radix = 1;
    int k;
    for (int i = 1; i <= d; i++) { // 按照位数进行d次排序
        for (int j = 0; j < 10; j++) {
            count[j] = 0; // 每次分配前清空计数器
        }
        for (int j = 0; j < 10; j++) {
            // 统计第i位上每个数字出现的数量
            k = (arr[j] / radix) % 10;
            count[k]++;
        }
        for (int j = 1; j < 10; j++) {
            // 得出count数组：count[j]为第i位上数字为0-j的元素的数量
            count[j] += count[j - 1];
        }
        for (int j = n - 1; j >= 0; j--) {
            // 将元素按照第i位上从小到大的顺序记录到tmp中
            k = (arr[j] / radix) % 10;
            tmp[count[k] - 1] = arr[j];
            count[k]--;
        }
        for (int j = 0; j < n; j++) {
            arr[j] = tmp[j];
        }
        radix *= 10;
    }
}